

Task 1
Approach
For task 1, the Uniform-Cost Search (UCS) algorithm is a search used to look for the shortest path from one place to another. UCS is an uninformed search that finds the path from source to the destination with the lowest cumulative cost. This is done by expanding unexplored nodes with the lowest distance cost. Therefore, a minimum heap, pq, is implemented for the search, which gives priority to the path that requires the least distance cost (distCost). Apart from this, several other dictionaries are initialised such as nodeDistance (stores path cost to the node), and pi (stores preceding node). Furthermore, a visited array is used to keep track of which nodes have been explored.

Task 2
Approach
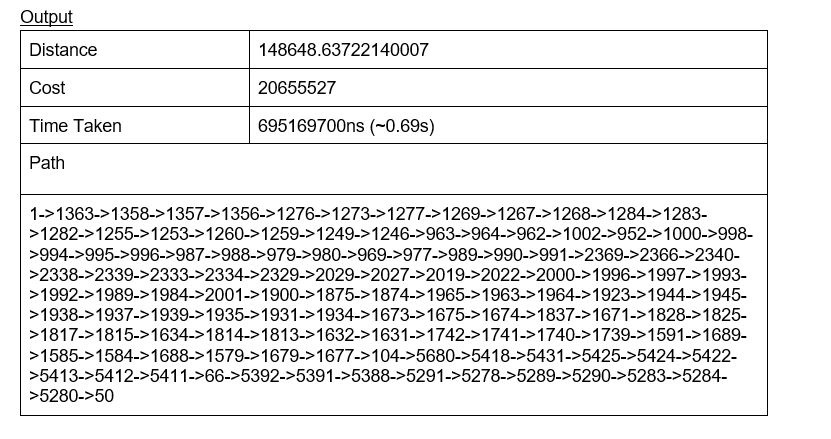
We are using uniform cost search with added constraints to take the energy cost into consideration, ensuring it does not exceed the stipulated energy budget.
We cannot simply find the path only by expanding the node with shortest distance because this will not guarantee that the energy constraint is met. Furthermore, we also cannot mark a node as visited upon exploring it once because we may need to explore the same node again in a different path (one which is longer but with less energy cost). Therefore, the new approach involves storing into the min heap, pq, not only the node value and distance as priority, but as a tuple of (node, energyCost) and distance as priority. Furthermore, as one node may be explored several times, it may also have several parents. Hence, a parent dictionary is used. parent uses (node, energyCost, distCost) as its key and stores the preceding node (parent node) as its value.
Therefore, we are able to explore multiple paths and still track the order of nodes traveled. Similarly, in the visited array, we will be storing (node, energyCost) to ensure a node can be visited more than once. To speed up the searching process, we will keep track of the minimum energy cost (minCost dictionary) to travel to each explored node. This is explained in the next paragraph.
Similar to task 1, the while loop has the same terminating conditions and logic. However, upon extracting the minimum (node, energyCost) based on distCost from pq, additional checks are performed. If energyCost to travel to this node is more than the current minimum energy cost, we do not bother exploring this (node, energyCost) tuple. This is because a (node, energyCost) tuple with both lower energyCost and distCost has already been explored as the pq uses distCost as priority. This ensures the shortest path and reduces the number of tuples we need to explore.
Another modification to that of task 1 is that during the visiting of child/neighbor nodes. If the energyCost to travel to the child/neighbor node exceeds the energy budget, we will not add this (neighborNode, energyCost) into pq.


Task 3
Approach
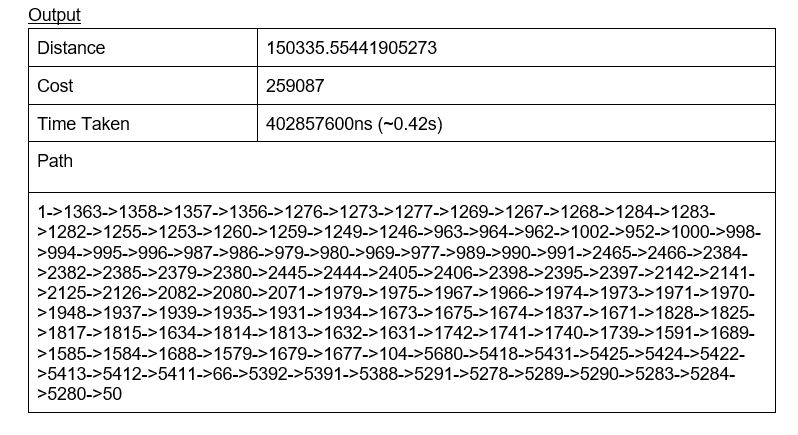
To solve this NYC instance, A star approach was used to find the shortest path with the least energy required to travel from the source to the destination. A star search is an informed search and uses both the cost of a path as well as heuristics to find the optimal solution. A star search is optimal and complete, which means that a guaranteed best solution can be found.
As the search enters a node, the cost of all the possible paths to the neighbor nodes are calculated. The search will proceed to the node that gives the lowest f(n) value. The f(n) function is calculated by adding g(n) and h(n). The cost g(n) refers to the cost from the start to the current node while h(n) is the heuristic based estimated cost for the current node to the destination node. .
For this problem, the heuristic function used is the Euclidean distance. Given two coordinates Ax1,y1 and Bx2,y2, the distance from A to B is calculated using the following formula,
(x2-x1)2+(y2-y1)2.
Conclusion
UCS and A* Search are both search algorithms that are both optimal and complete. This means that the resulting path will generally be unique and we can expect the same results for both algorithms given the same input.
As such, both tasks 2 and 3 resulted in the same path and cost. However, it is worth noting that due to a heuristic function being factored into the search, less nodes were expanded for A* search, resulting in less time (~100 times faster) taken to find the optimal path/cost.
By having a heuristic function, the algorithm performed much better as it allows the search to make better informed node expansion decisions and eliminate certain options that led to paths which were nowhere near the goal. This greatly reduced the runtime complexity of the algorithm.
